

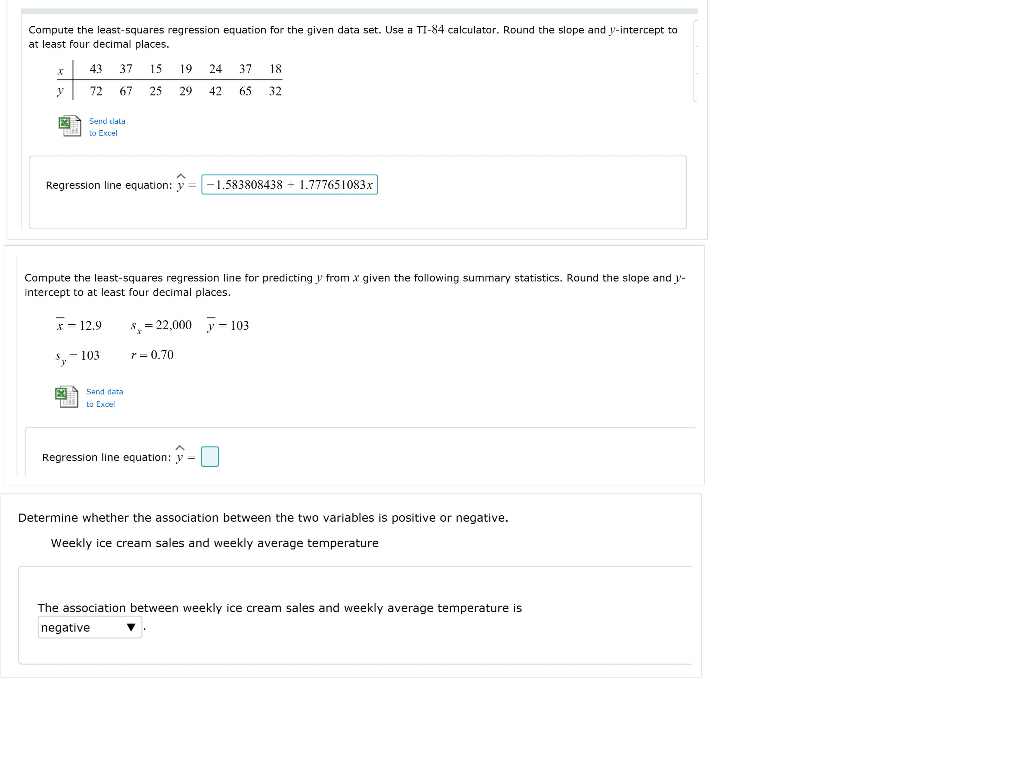
#Least squares regression line equation calculator plus
One plus two plus two plus three divided by four, Here, so the sample mean for x, it's easy to calculate In red so that you know that's what is going on Sample standard deviation for x are here in red, and actually let me box these off We clearly have the fourĭata points plotted, but let's plot the statistics for x. So before I do that, let's just visualize some of the statistics that we have here for these data points. On this video is build on this notion and actuallyĬome up with the equation for the least squares We got an r of 0.946, which means we have a fairly If r is equal to zero, you don't have a correlation, but for this particular bivariate dataset, One, you have a perfect negative correlation, and And as we said, if r is equal to one, you have a perfect positive correlation. The product of the z scores for each of those pairs. In that video we saw all it is is an average of Keep in mind that our linear regression calculator does not verify the assumptions of linear regression! You have to check them by yourself - at least remember to take a look at residuals to verify if they are independent, normally distributed, and homoscedastic (i.e., whether they have constant variance).- In previous videos, we took this bivariate data and weĬalculated the correlation coefficient, and justĪs a bit of a review, we have the formula here, and it looks a bit intimidating, but There you can set the number of significant figures.
If you don't know what the coefficient of determination R² is, check the R squared calculator. Recall that R² ranges from 0 to 1, and the closer it is to 1, the better the fit. It tells you what proportion of the variance in the dependent variable y is explained by the model. Moreover, we tell you the R² of the fitted model.Below the plot you can find the linear regression equation for your data.We will show you the scatter plot of your data with the regression line.The calculator needs at least 3 points to fit the linear regression model to your data points. To use the linear regression calculator, follow the steps below: We call such a point the center of mass of the set of data points. Namely, the intercept coefficient b is such that the regression line passes through the point whose horizontal coefficient is equal to the mean of the x values, and the vertical coefficient is equal to the mean of the y values. It has one more interesting property, which is related to the mean values of our observations. It isn't hard to note that the intercept coefficient b indicates the point on the vertical axis through which the fitted line passes. sd(x) is the standard deviation of x and.corr(x, y) is the correlation between x and y.Interestingly, we can express the slope a in terms of the standard deviations of x and y and of their Pearson correlation. If a = 0, then there is no relationship between the two variables in question: the value of y is the same (constant) for all values of x.We say there is a negative relationship between the two variables: as one increases, the other decreases. If a We say there is a positive relationship between the two variables: as one increases, the other increases as well. If a > 0, then y increases by a units whenever x increases by 1 unit.

Indeed, let's take a look at the following simple calculation:Ī * (x + 1) + b = (a * x + b) + a = y + a.
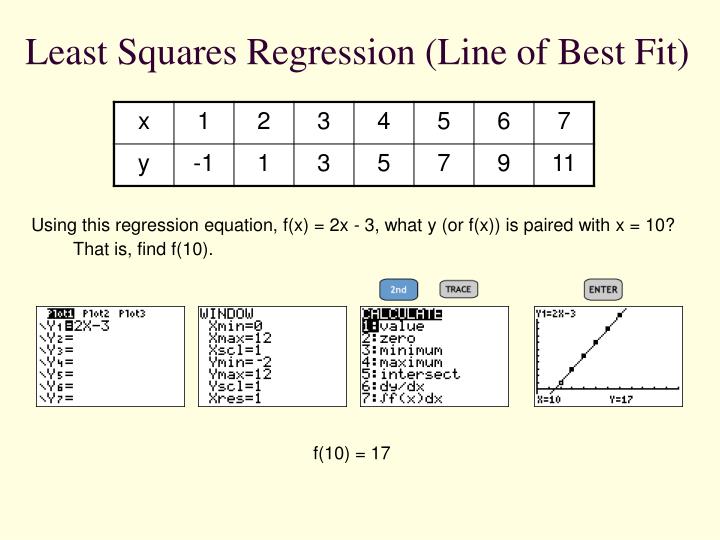
It describes how much the dependent variable y changes (on average!) when the incoefficient of determination**, dependent variable x changes by one unit**. The coefficient a is the slope of the regression line. A simple example is when we want to predict the weights of students based on their heights, or in chemistry, where linear regression is used in the calculation of the concentration of an unknown sample.īe careful, as in some situations simple linear regression may not be the right model! If your data seem to follow a parabola rather than a straight line, then you should try using our quadratic regression calculator, if they rather resemble a cubic (degree three) curve, try the cubic regression calculator, while if your data come from a process characterized by exponential growth, try the exponential regression calculator instead. In other words, when we have a set of two-dimensional data points, linear regression describes the (non-vertical) straight line that best fits these points. Linear regression is a statistical technique that aims to model the relationship between two variables (one variable is called explanatory/independent and the other is dependent) by determining a linear equation that best predicts the values of the dependent variable based on the values of the independent variable.


 0 kommentar(er)
0 kommentar(er)
